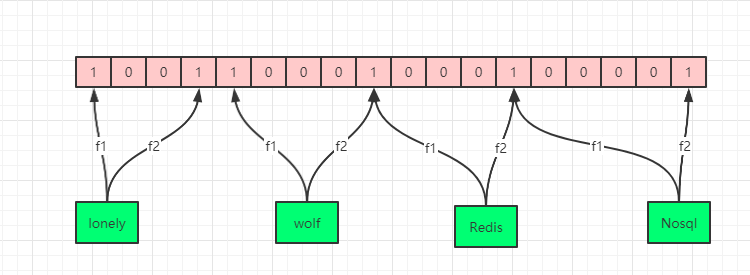
JPS路径搜索算法

这周主要根据jps路径搜索算法的定义，尝试实现jps算法。

jps算法全称是jump point search，它可以看做A* 的改进算法，首先简要简绍A*算法原理

A*算法

A*算法的一些概念

G：当前位置距离原点已经走过的距离

H：当前位置距离终点的预估距离

F：F=G+H，作为每个点的权重

搜索方法

将原点加入openlist中，每当openlist有值就遍历openlist中的点，每次遍历首先找出F值最小的节点作为当前点，遍历后的加入另一个列表防止重复遍历。

遍历当前点的邻居，没有遍历过的点设置G和H值，设置父节点，之后加入openlist中。

由此往复这个过程，直到找到目标点。

在A*算法的寻路过程中将很多畅通无阻的点也加入了openlist，这是可以改进的

JPS算法

A*将各个邻居都加入了openlist，之后算的F值，实际上能舍弃很多不需要的节点。

jps算法引入了一些新概念。

JPS算法增加的概念

跳点

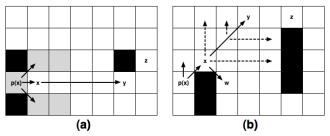
对于跳点的理解如图a，点y对于p(x)是跳点，p(x)与点y之间没有障碍，畅通无阻，可直接从p(x)跳跃到y点。不需要像A*算法一样，将右上方，x，右下方都加进openlist来找最小的权重值F的节点。

jps的大致步骤如图b

由p(x)点出发寻找一点，首先向p(x)的上下左右方向各找跳点，等找到地图边界或者遇到障碍就返回。之后向四个对角线方向各进一步，如果是跳点加入openlist后直接返回；如果不是接着找上下左右四个方向的跳点，将跳点加入openlist。

根据上面说的得出结论：

• 有强迫邻居的节点是跳点
• 当前节点是个跳转点。当前节点的上一个跳点在对角线方向，后一个跳点在当前节点的正方向（也就是拐弯了），那么当前节点也是跳点。

舍弃不需要的邻居节点

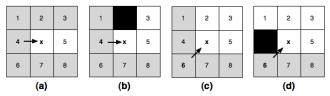
（x表示当前节点，黑色方块表示障碍）

1. 在没有障碍情况下，只考虑直行情况

   图a，节点4到x，可舍弃123678节点。

   图c，节点6到x，可舍弃1478节点。

2. 存在障碍情况下，需要考虑强制节点

   图b，节点3对于节点x是强制节点。

   图d，节点1对于节点x是强制节点。

强制邻居

图b，从x到节点3必须经过x，3就是x的强制邻居。

图d，同上。

搜索方法

第一步

查找起点四个方向的跳点，之后搜索对角线四个方向，在四个节点中，分别找当前对角线向量x，y分量方向的跳点。当找到跳点，加入openlist。之后各个对角线方向的点各前进一步，如果找到跳点就加入openlist后直接返回；如果不是跳点就接着按x，y方向找跳点，直到碰到障碍，或者到达地图边界。

第二步

while(openlist.Length>0)，每次找到F最低的节点，从openlist中移除，之后和第一步 类似，直到找到目标点。

JPS的优化

• 剪枝优化，不是论文中的减去邻居节点，而是如图一b的从x到y到z中的y节点可以不加入openlist中，只保留x与z节点。之后进行判断，填充y节点到路径中。这样就可以避免y节点不必要的运算。
• 位运算，0表示可行走，1表示障碍。将每行每列就能用0和1来表示。判断是否有障碍就能提升速度。
• jps预处理，也称JPS+，略，不支持可移动障碍物。